TAMUNA: Doubly Accelerated Federated Learning with Local Training, Compression, and Partial Participation#
Note: If you use this baseline in your work, please remember to cite the original authors of the paper as well as the Flower paper.
Paper: arxiv.org/abs/2302.09832
Authors: Laurent Condat, Ivan Agarský, Grigory Malinovsky, Peter Richtárik
Abstract: In federated learning, a large number of users collaborate to learn a global model. They alternate local computations and communication with a distant server. Communication, which can be slow and costly, is the main bottleneck in this setting. In addition to communication-efficiency, a robust algorithm should allow for partial participation, the desirable feature that not all clients need to participate to every round of the training process. To reduce the communication load and therefore accelerate distributed gradient descent, two strategies are popular: 1) communicate less frequently; that is, perform several iterations of local computations between the communication rounds; and 2) communicate compressed information instead of full-dimensional vectors. We propose TAMUNA, the first algorithm for distributed optimization and federated learning, which harnesses these two strategies jointly and allows for partial participation. TAMUNA converges linearly to an exact solution in the strongly convex setting, with a doubly accelerated rate: it provably benefits from the two acceleration mechanisms provided by local training and compression, namely a better dependency on the condition number of the functions and on the model dimension, respectively.
About this baseline#
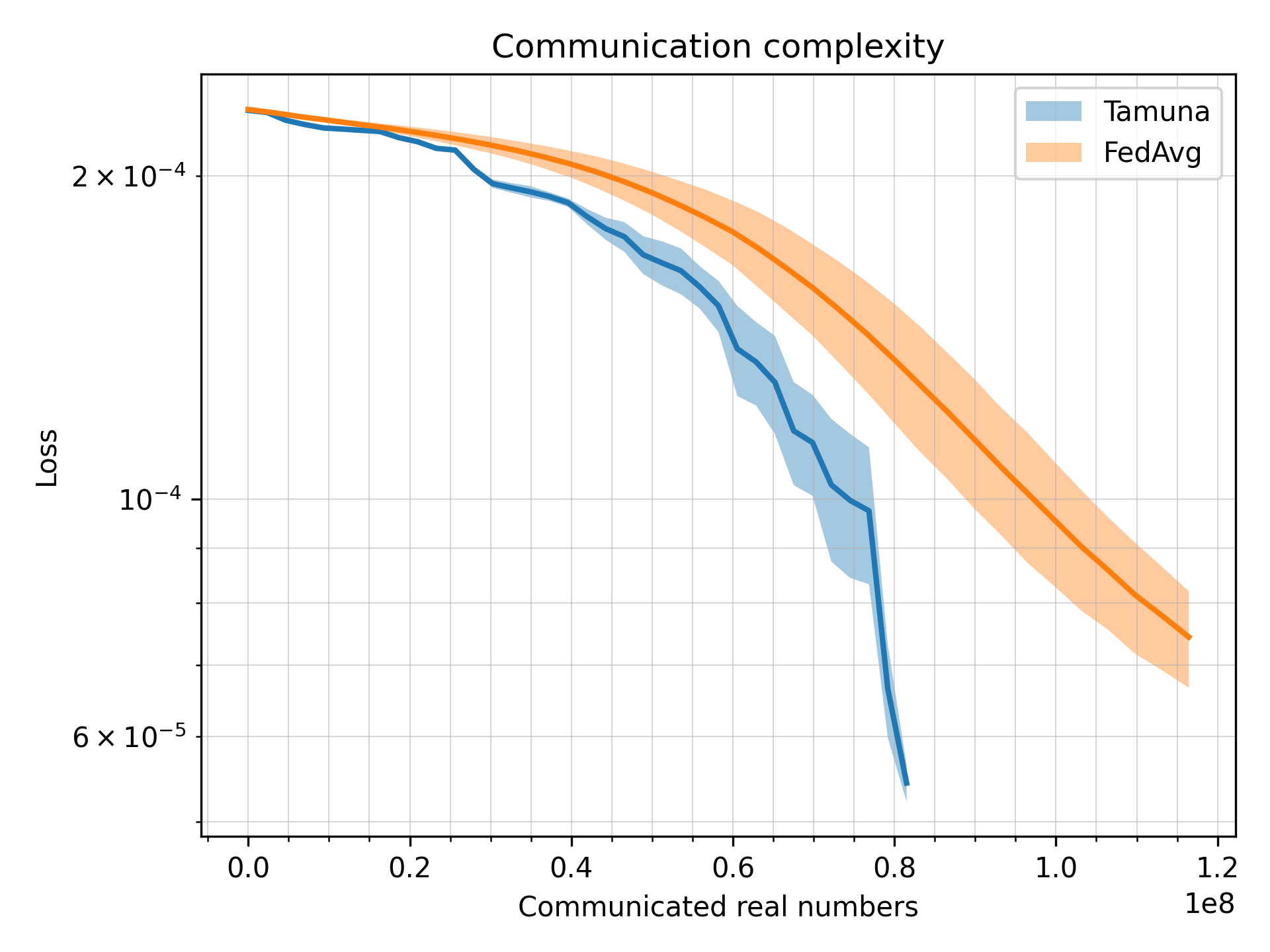
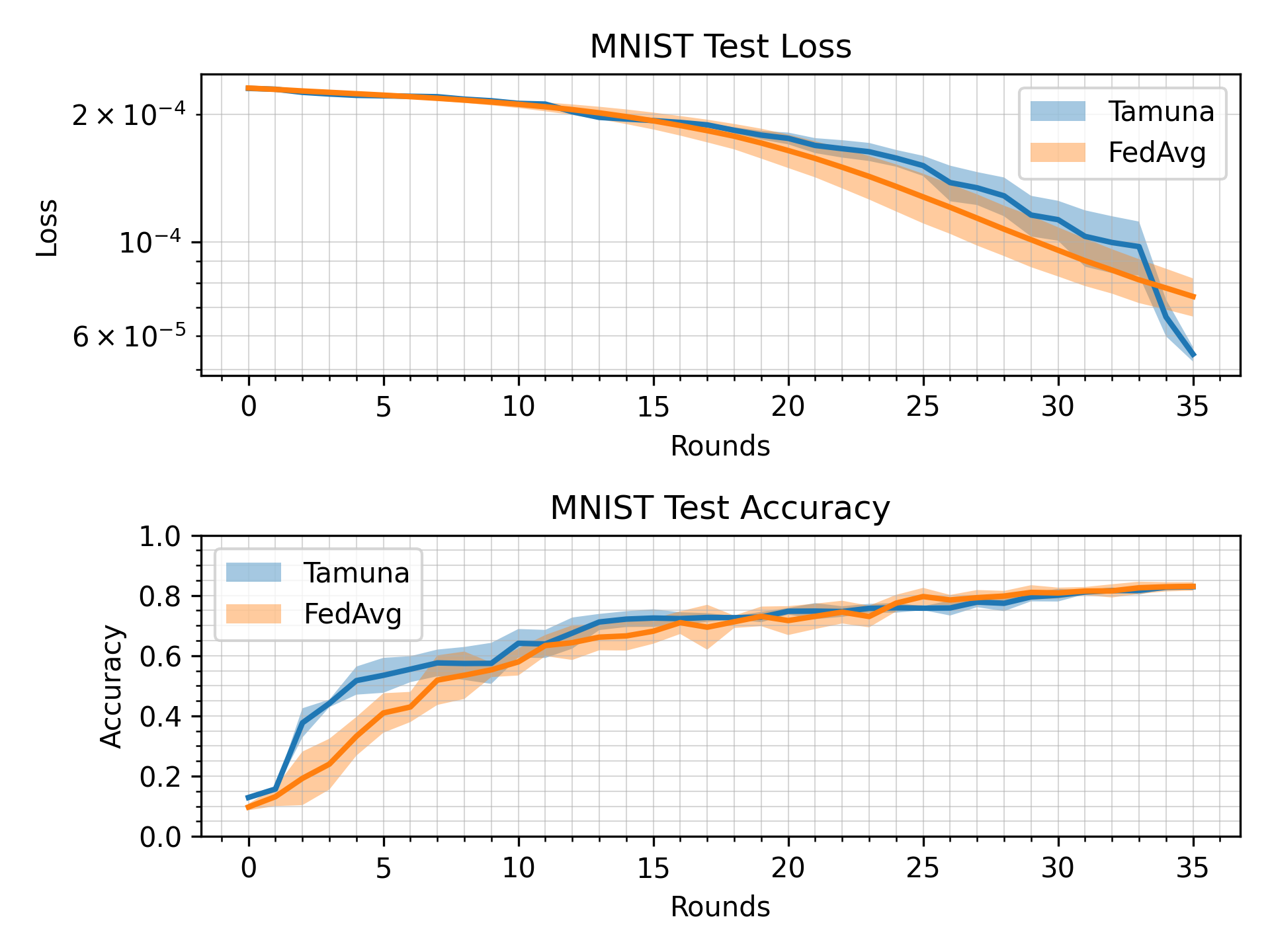
What’s implemented: The code in this directory compares Tamuna with FedAvg. It produces three plots comparing loss, accuracy and communication complexity of the two algorithms.
Datasets: MNIST
Hardware Setup: By default, the experiments expect at least one gpu, but this can be changed to cpu only by specifying client and server devices. Default setup less than 5 GB of dedicated GPU memory.
Contributors: Ivan Agarský github.com/Crabzmatic, Grigory Malinovsky github.com/gsmalinovsky
Experimental Setup#
Task: image classification
Model:
As described in (McMahan, 2017): Communication-Efficient Learning of Deep Networks from Decentralized Data (arxiv.org/abs/1602.05629)
Layer |
Input Shape |
Output Shape |
Param # |
Kernel Shape |
|
|---|---|---|---|---|---|
Net |
[1, 28, 28] |
[10] |
– |
– |
|
Conv2d |
[1, 28, 28] |
[32, 26, 26] |
832 |
[5, 5] |
|
MaxPool2d |
[32, 26, 26] |
[32, 14, 14] |
– |
[2, 2] |
|
Conv2d |
[32, 14, 14] |
[64, 12, 12] |
51,264 |
[5, 5] |
|
MaxPool2d |
[64, 12, 12] |
[64, 7, 7] |
– |
[2, 2] |
|
Linear |
[3136] |
[512] |
1,606,144 |
– |
|
Linear |
[512] |
[10] |
5,130 |
– |
Total trainable params: 1,663,370
Dataset: By default, training split of MNIST dataset is divided in iid fashion across all 1000 clients, while test split stays on the server for centralized evaluation. Training dataset can also be divided using power law by setting dataset.iid to False in base.yaml config.
Training Hyperparameters:
Hyperparameter |
Description |
Default value |
|---|---|---|
|
Number of active/participating clients each round. |
10 |
|
Number of total clients. |
1000 |
|
Number of training rounds, this does not include local training epochs. |
35 |
|
This describes the level of sparsity in the compression mask, needs to be between 2 and |
4 |
|
Describes the probability of server communication while doing local training, in other words, clients will in expectation do 1/ |
0.333 |
|
Weight of uplink (client to server) communication when calculating communication complexity. |
1 |
|
Weight of downlink (server to client) communication when calculating communication complexity. |
1 |
|
Learning rate for client local training. |
0.01 |
|
Learning rate for updating control variates, needs to be between |
0.246 |
|
How many times should the training be repeated from the beginning for both Tamuna and FedAvg. Values bigger than 1 will produce plots that show how the randomness affects the algorithms. |
3 |
Environment Setup#
This requires pyenv and poetry already installed.
# set local python version via pyenv
pyenv local 3.10.6
# then fix that for poetry
poetry env use 3.10.6
# then install poetry env
poetry install
Running the Experiments#
Default experimental setup in defined in conf/base.yaml, this can be changed if needed.
poetry run python -m tamuna.main
Running time for default experimental setup is around 13min on Intel Core i5-12400F and Nvidia GeForce RTX 3060 Ti,
while the CPU-only version, which can be found in conf/base-cpu.yaml, takes around 20min.
Expected Results#
The resulting directory in ./outputs/ should contain (among other things) communication_complexity.png and loss_accuracy.png.